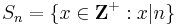Divisor topology

In mathematics, more specifically general topology, the divisor topology is an example of a topology given to the set X of positive integers that are greater than or equal to two, i.e., X = {2, 3, 4, 5, …}. The divisor topology is the poset topology for the partial order relation of divisibility on the positive integers.

To give the set X a topology means to say which subsets of X are "open", and to do so in a way that the following axioms are met:^[1]

1. The union of open sets is an open set.
2. The finite intersection of open sets is an open set.
3. The set X and the empty set ∅ are open sets.

Construction

The set X and the empty set ∅ are required to be open sets, and so we define X and ∅ to be open sets in this topology. Denote by Z⁺ the set of positive integers, i.e., the set of positive whole number greater than or equal to one. Read the notation x|n as "x divides n", and consider the sets

Then the set S_n is the set of divisors of n. For different values of n, the sets S_n are used as a basis for the divisor topology.^[1]

The open sets in this topology are the lower sets for the partial order defined by x ≤ y if x | y.

Properties

• The set of prime numbers is dense in X. In fact, every dense open set must include every prime, and therefore X is a Baire space.^[1]
• X is a Kolmogorov space that is not T1. In particular, it is non-Hausdorff.
• X is second countable.
• X is connected and locally connected.
• X is not compact, since the basic open sets S_n comprise an infinite covering with no finite subcovering. X is not locally compact.
• The closure of a point in x is the set of all multiples of x.

See also

• Zariski topology: A topology on the integers whose open sets are the complements of prime ideals.

References